Jeder kann coden / Programmieren & TicTacToe / C# Einführung / Operatoren Übersicht
Grundlagen Boolesche Operatoren¶

|
|
|
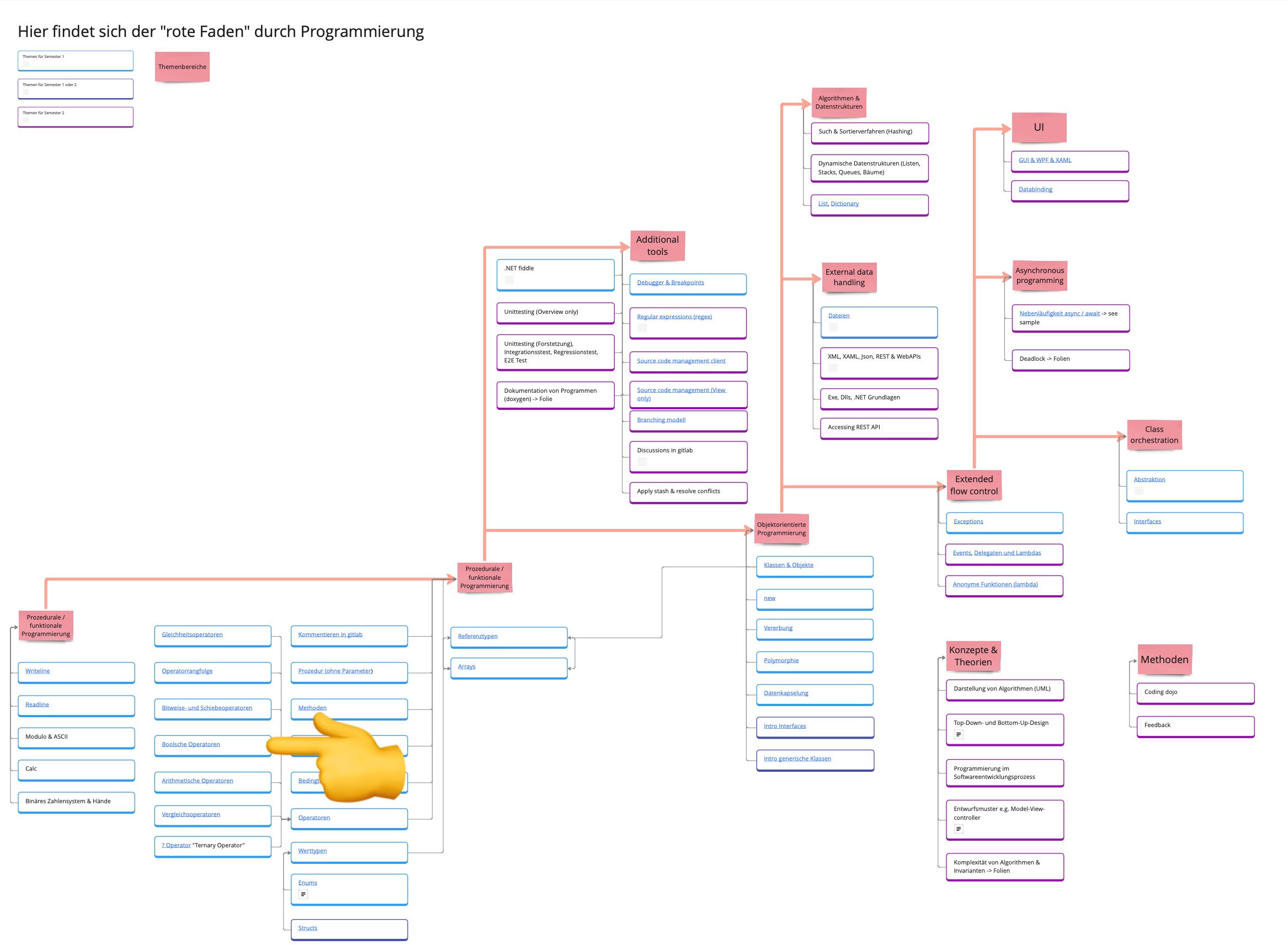
Link zur Microsoft Dokumentation Link zum roten Faden auf Miro Link zu Tutorial auf w3schools |
Boolesche Algebra¶
1. Einleitung in die boolsche Algebra¶
Definition
- Mathematisches System für Wahrheitswerte
- Grundlage für digitale Logik und Programmierung
Bedeutung in der Informatik
- Zentral für digitale Schaltungen
- Relevant in Datenbankabfragen und Algorithmen
Geschichte
- Entwickelt von George Boole im 19. Jahrhundert
- Grundlage für moderne Computertechnik
Anwendungsbeispiele
- Digitale Schaltungen: Logikgatter in Hardware
- Suchalgorithmen: Datenfilterung in Datenbanken
- Programmiersprachen: Steuerung des Programmflusses
Ausführliche Erklärung...
Die boolesche Algebra ist ein mathematisches System, das auf den Wahrheitswerten basiert und die logische Verarbeitung von Informationen ermöglicht. Sie ist die Grundlage für digitale Schaltungen und Programmierung.Bedeutung in der Informatik Boolesche Algebra spielt eine zentrale Rolle in der Computerwissenschaft, insbesondere in der digitalen Logik, Datenbankabfragen, Programmierung und Algorithmusentwicklung. Sie ermöglicht es, komplexe logische Bedingungen zu formulieren und zu verarbeiten.
Geschichte George Boole, ein englischer Mathematiker, entwickelte im 19. Jahrhundert die Grundprinzipien der booleschen Algebra. Seine Arbeit führte zur Formulierung der booleschen Operationen, die für die moderne Computertechnik von entscheidender Bedeutung sind.
- Anwendungsbeispiele
- Boolesche Algebra wird in einer Vielzahl von Anwendungen eingesetzt, darunter:
- Digitale Schaltungen: Logikgatter, die in der Hardwareentwicklung verwendet werden.
- Suchalgorithmen: Bedingungen zur Filterung von Daten in Datenbanken.
- Programmiersprachen: Verwendung von booleschen Ausdrücken zur Steuerung des Programmflusses.
- Boolesche Algebra wird in einer Vielzahl von Anwendungen eingesetzt, darunter:
2. Boolesche Operatoren in C#¶
2.1 AND-Operator (&&)¶
Erklärung:
Der AND-Operator (&&) gibt true zurück, wenn beide Operanden true sind. Dies ist besonders nützlich, um komplexe Bedingungen zu formulieren.
💡 Dieser Operator hat Laufzeitvorteile, da er den zweiten Operanden nur auswertet, wenn der erste true ist. Er wird daher auch bedingter Operator genannt.
bool a = true;
bool b = false;
bool result = a && b; // result ist false
2.2 OR-Operator (||)¶
Erklärung:
Der OR-Operator (||) gibt true zurück, wenn mindestens einer der Operanden true ist. Dies ermöglicht die Definition von Alternativen in logischen Ausdrücken.
💡 Dieser Operator hat Laufzeitvorteile, da er den zweiten Operanden nur auswertet, wenn der erste false ist. Er wird daher ebenfalls bedingter Operator genannt.
bool a = true;
bool b = false;
bool result = a || b; // result ist true
2.3 NOT-Operator (!)¶
Erklärung:
Der NOT-Operator (!) kehrt den booleschen Wert um. Wenn der Operand true ist, wird er zu false und umgekehrt.
bool a = true;
bool result = !a; // result ist false
2.4 Bitwise AND-Operator (&)¶
Erklärung:
Der bitweise AND-Operator (&) führt eine bitweise AND-Operation durch. Dies ist nützlich, um mit Ganzzahlen auf Bit-Ebene zu arbeiten.
int a = 5; // (0101)
int b = 3; // (0011)
int result = a & b; // result ist 1 (0001)
2.5 Bitwise OR-Operator (|)¶
Erklärung:
Der bitweise OR-Operator (|) führt eine bitweise OR-Operation durch, die die Bits beider Operanden vergleicht.
int a = 5; // (0101)
int b = 3; // (0011)
int result = a | b; // result ist 7 (0111)
2.6 Bitwise XOR-Operator (^)¶
Erklärung:
Der bitweise XOR-Operator (^) gibt true zurück, wenn die Operanden unterschiedlich sind. Dies ist nützlich, um Unterschiede zwischen zwei Zahlen zu identifizieren.
int a = 5; // (0101)
int b = 3; // (0011)
int result = a ^ b; // result ist 6 (0110)
int c = result ^ b;
Console.WriteLine(result + " " + c);
6 5
3. Distributivgesetz¶
Erklärung: Das Distributivgesetz in der booleschen Algebra beschreibt, wie sich Operationen auf eine bestimmte Weise verteilen. Es wird formuliert als:
- $( A \land (B \lor C) = (A \land B) \lor (A \land C) )$
- $( A \lor (B \land C) = (A \lor B) \land (A \lor C) )$
Beispiele:
- AND über OR:
bool A = true;
bool B = false;
bool C = true;
bool result = A && (B || C); // result ist true
// Entsprechend dem Distributivgesetz:
bool result2 = (A && B) || (A && C); // result2 ist true
- OR über AND:
bool A = true;
bool B = false;
bool C = false;
bool result = A || (B && C); // result ist true
// Entsprechend dem Distributivgesetz:
bool result2 = (A || B) && (A || C); // result2 ist true
4. De Morgansche Gesetze¶
Die beiden Gesetze lauten:
- $¬(A∧B)=¬A∨¬B¬(A∧B)=¬A∨¬B$
- $¬(A∨B)=¬A∧¬B¬(A∨B)=¬A∧¬B$
Bedeutung¶
- Das erste Gesetz besagt, dass die Negation eines AND-Ausdrucks gleich der Disjunktion (OR) der Negationen der einzelnen Terme ist.
- Das zweite Gesetz besagt, dass die Negation eines OR-Ausdrucks gleich der Konjunktion (AND) der Negationen der einzelnen Terme ist.
Beispiele in C#¶
- Erstes Gesetz:
bool A = true;
bool B = false;
bool result = !(A && B); // result ist true
// Entsprechend dem De Morganschen Gesetz:
bool result2 = !A || !B; // result2 ist true
- Zweites Gesetz:
bool A = true;
bool B = false;
bool result = !(A || B); // result ist false
// Entsprechend dem De Morganschen Gesetz:
bool result2 = !A && !B; // result2 ist false
Diese Gesetze sind sehr nützlich in der Logik und der Programmierung, insbesondere bei der Vereinfachung von booleschen Ausdrücken und der Analyse von Bedingungen.
4. Komplexe boolesche Ausdrücke¶
Erklärung: Komplexe boolesche Ausdrücke können durch die Kombination mehrerer Operatoren gebildet werden. Dabei ist die Reihenfolge der Operationen wichtig.
bool a = true;
bool b = false;
bool c = true;
bool result = a && (b || c); // result ist true
5. Anwendungen der booleschen Algebra¶
Erklärung: Boolesche Ausdrücke sind grundlegend für Kontrollstrukturen in der Programmierung, wie if-Anweisungen und Schleifen. Sie steuern den Fluss von Programmen und ermöglichen die Ausführung bestimmter Codeabschnitte unter bestimmten Bedingungen.
Ein Beispiel könnte die Verwendung von booleschen Ausdrücken in einem Such- oder Sortieralgorithmus sein, wo Bedingungen über die zu vergleichenden Elemente entscheiden, wie die Iterationen stattfinden.