• Htw
  • Anleitung zur Prüfungsgruppenanmeldung
• Programming
  • Zahlensysteme und Zeichendarstellung
  • Objektorientierte Programmierung
  • Programmieren 1
  • Programmierung und Tic-Tac-Toe
  • Was sind Web APIs?
  • Abstract
    • Jeder kann coden
    • Jeder kann coden
  • Cmdline
    • Bash
    • 💡 Erstes Skript & sandbox
    • Navigation durch den Verzeichnisbaum
    • Howtos
    • Linux-Skript zur Systeminformationenserfassung
    • Kommandozeile
  • Csharp
    • Csharp_introduction
      • Arrays in C#
      • Komplexere Datenstrukturen
      • Bedingte Anweisungen
      • Prozeduren und Funktionen
      • Schleifen
      • Operatoren
      • Mit Strings arbeiten
      • Das Konzept einer Variablen
    • Einführung in C#
    • Eisbrecher
    • Framework
      • Exceptions
      • Dateioperationen in C#
      • .NET System.Random
      • Reguläre Ausdrücke
      • Wpf
        • Einführung in die Grundlagen von WPF und C#
        • Data Binding mit WPF und C#
    • Oop
      • Zugriffsmodifizierer in C#
      • Grundlagen der objektorientierten Programmierung (OOP) in C#
      • Objektorientierte Programmierung in C# Samples
      • 💡 Vergleich von Objekten
      • Konstruktoren in C#
      • Beispiel: Spielfeldmanagement in C#
      • Properties (Attribute) in C#
    • Procedural-functional
      • Arrays in C#
      • Grundlagen Boolesche Operatoren
      • Bedingte Anweisungen in C#
      • Bedingte Anweisungen & TicTacToe
      • Enums in C#
      • C# - Struktur eines Programms
      • Schleifen in C#
      • Schleifen & TicTacToe
      • Prozeduren, Funktionen und Methoden in C#
      • Numerische Gleitkomma-Typen
      • Ganzzahlige numerische Typen
      • Grundlagen weiterer Operatoren
      • Referenztypen und Werttypen in C#
      • String Typen in C#
      • Structs in C#
      • Grundlagen C# ReadLine
      • Grundlagen C# WriteLine
      • C# WriteLine Samples
      • C# WriteLine & TicTacToe
    • Tools
      • Debugger und Breakpoints
      • Entwicklungswerkzeuge für Programmierung
• Tools
  • Quellcodeverwaltung mit GIT
  • Visual Studio für Mac ist tot – was nun?

Jeder kann coden

Zahlensysteme und Zeichendarstellung

In der Programmierung spielen verschiedene Zahlensysteme eine wichtige Rolle. Hier sind die wichtigsten:

1. Dezimalsystem (Basis 10)

• Dies ist das übliche Zahlensystem, das im täglichen Leben verwendet wird.
• Es besteht aus den Ziffern 0 bis 9.
• Jede Stelle einer Zahl repräsentiert eine Potenz von 10.
• Beispiel: Die Zahl 345 bedeutet $3 \times 10^2 + 4 \times 10^1 + 5 \times 10^0$.

2. Binärsystem (Basis 2)

• Das Binärsystem verwendet nur die Ziffern 0 und 1.
• Es ist das grundlegende Zahlensystem in Computern, da sie intern mit elektrischen Zuständen (Ein/Aus, 1/0) arbeiten.
• Beispiel: Die Binärzahl 1011 bedeutet $1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 11$.

3. Hexadezimalsystem (Basis 16)

• Das Hexadezimalsystem verwendet die Ziffern 0 bis 9 und die Buchstaben A bis F (für die Werte 10 bis 15).
• Es ist in der Programmierung häufig, weil es sich leicht in Binärzahlen umwandeln lässt.
• Beispiel: Die Hexadezimalzahl 1F bedeutet $1 \times 16^1 + F \times 16^0 = 31$.

4. Oktalsystem (Basis 8)

• Das Oktalsystem verwendet die Ziffern 0 bis 7.
• Es wurde früher in der Programmierung verwendet, insbesondere bei frühen Computersystemen.
• Beispiel: Die Oktalzahl 17 bedeutet $1 \times 8^1 + 7 \times 8^0 = 15$.

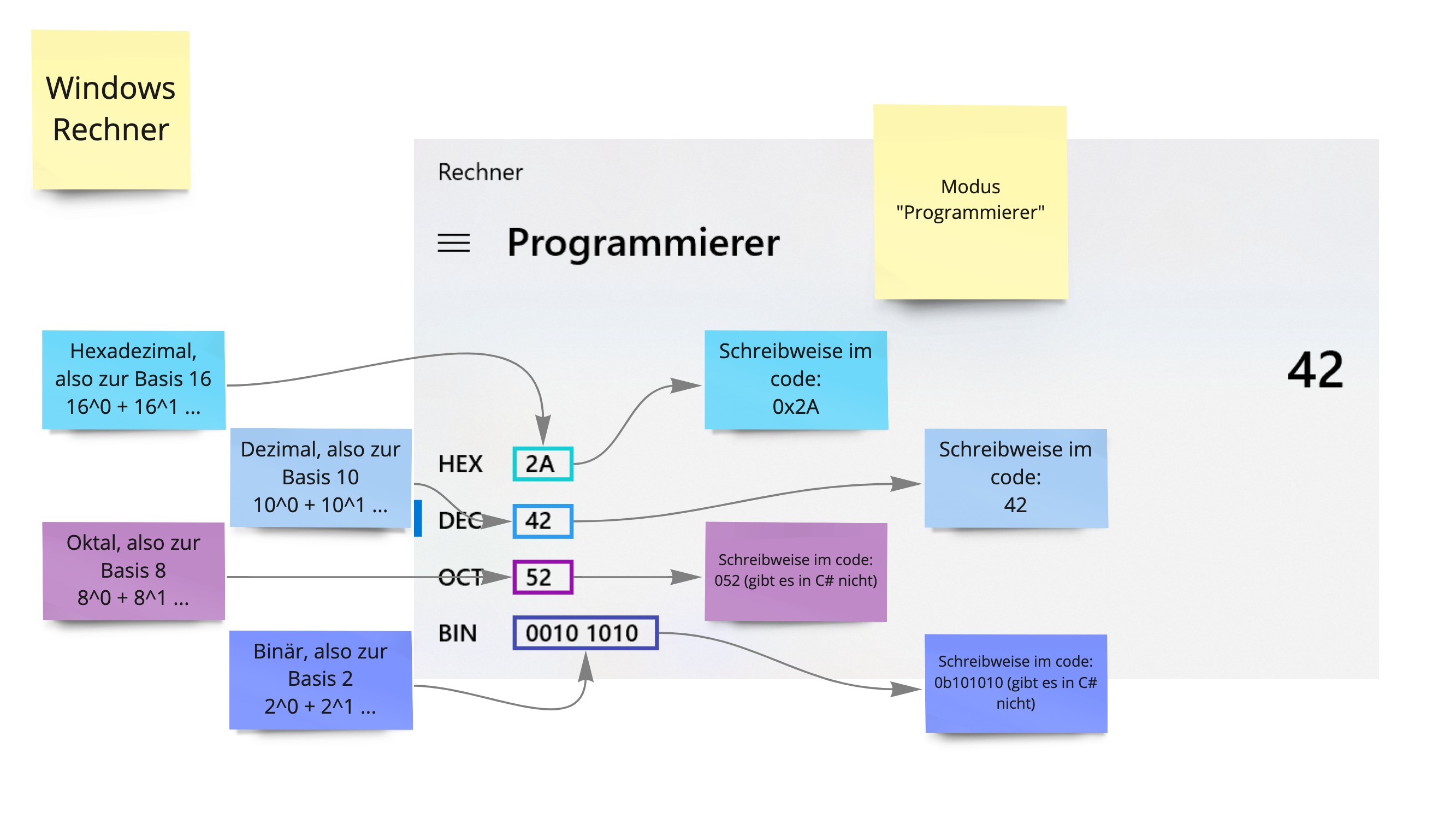
Windows Rechner (Taschenrechner)

Die verschiedenen Zahlensysteme kann man auch beispielsweise im Windows Rechner im Modus "Programmierer" nachvollziehen:

Spiel mit 10 Fingern

Mit den Fingern kann man tatsächlich im Binärsystem zählen. Dabei repräsentiert jeder Finger einen Bit (0 oder 1). Wenn ein Finger ausgestreckt ist, zählt er als 1, und wenn er eingeklappt ist, zählt er als 0. Insgesamt hat man 10 Finger, was 10 Bits entspricht.

• 10 Bits können Werte von 0 bis $2^{10} - 1$ darstellen, also von 0 bis 1023.
• Beispiel:
  • Alle Finger eingeklappt: $0000000000$ im Binärsystem = 0 im Dezimalsystem.
  • Nur der Daumen der rechten Hand ausgestreckt: $0000000001$ im Binärsystem = 1 im Dezimalsystem.
  • Daumen und Zeigefinger der rechten Hand ausgestreckt: $0000000011$ im Binärsystem = 3 im Dezimalsystem.
  • Alle Finger ausgestreckt: $1111111111$ im Binärsystem = 1023 im Dezimalsystem.

Modulo %

• Definition: Modulo ist der Rest einer Division zweier Zahlen.
• Notation: $a\ mod\ n = r$, wobei $r$ der Rest ist, wenn $a$ durch $n$ geteilt wird.
• Beispiel: $10\ mod\ 3 = 1$ ($10$ geteilt durch $3$ ergibt $3$ mit einem Rest von $1$).
• Eigenschaften:
  • Immer kleiner als der Divisor $(n)$.
  • Wird oft in der Informatik und Zahlentheorie verwendet (z. B. bei der Bestimmung von Uhrzeiten, in Algorithmen).
• Anwendung: Zyklische Strukturen, wie Uhrzeitberechnungen oder Hash-Funktionen.

Nochmal zum Nachlesen...

Modulo ist eine mathematische Operation, die den Rest einer Division zweier Zahlen bestimmt. Sie wird häufig in der Informatik und Mathematik verwendet, um zyklische oder periodische Phänomene zu beschreiben. Die Modulo-Operation wird oft durch das Zeichen % dargestellt.

Beispiel:

Wenn du $a \mod b$ berechnest, dann teilst du $a$ durch $b$ und nimmst den Rest dieser Division.

Beispielrechnung:

• $10 \mod 3$ bedeutet, dass du 10 durch 3 teilst.
• Das Ergebnis der Division ist $10 \div 3 = 3$ mit einem Rest von 1.
• Somit ist $10 \mod 3 = 1$.

In diesem Fall ist 3 der Divisor, und 1 ist der Rest, den die Modulo-Operation liefert.

Eigenschaften:

1. Zyklisch: Modulo wird oft verwendet, um zyklische Abläufe zu modellieren, wie zum Beispiel Uhrzeiten oder Kalender. Bei einer Uhr mit 12 Stunden entspricht $14 \mod 12$ der 2, weil 14 Stunden 12 Stunden plus 2 Stunden sind.

2. Ganzzahlige Division: Modulo ist eng mit der ganzzahligen Division verknüpft, bei der der Quotient ignoriert und nur der Rest betrachtet wird.

3. Negative Zahlen: Der Modulo-Operator kann auch auf negative Zahlen angewendet werden, aber das Verhalten kann je nach Definition unterschiedlich sein. Beispielsweise könnte $-10 \mod 3$ entweder $-1$ oder $2$ sein, je nachdem, wie die Modulo-Operation definiert ist.

Anwendung:

• Programmierung: Modulo wird oft verwendet, um eine Zahl in einem bestimmten Bereich zu halten, beispielsweise, um sicherzustellen, dass ein Index innerhalb eines Arrays bleibt.
• Kryptographie: Modulo spielt eine zentrale Rolle in Verschlüsselungsalgorithmen wie RSA, da es hilft, mit großen Zahlen umzugehen und periodische Muster zu erzeugen.
• Zahlenrätsel: Modulo hilft auch, gewisse Muster oder Regelmäßigkeiten in Zahlen zu erkennen, wie etwa, ob eine Zahl durch eine andere teilbar ist (zum Beispiel ist eine Zahl durch 3 teilbar, wenn $n \mod 3 = 0$).

Zusammengefasst: Die Modulo-Operation gibt den Rest einer Division an und ist ein nützliches Werkzeug, um mit periodischen Strukturen zu arbeiten.

Bytes und die Darstellung von Text

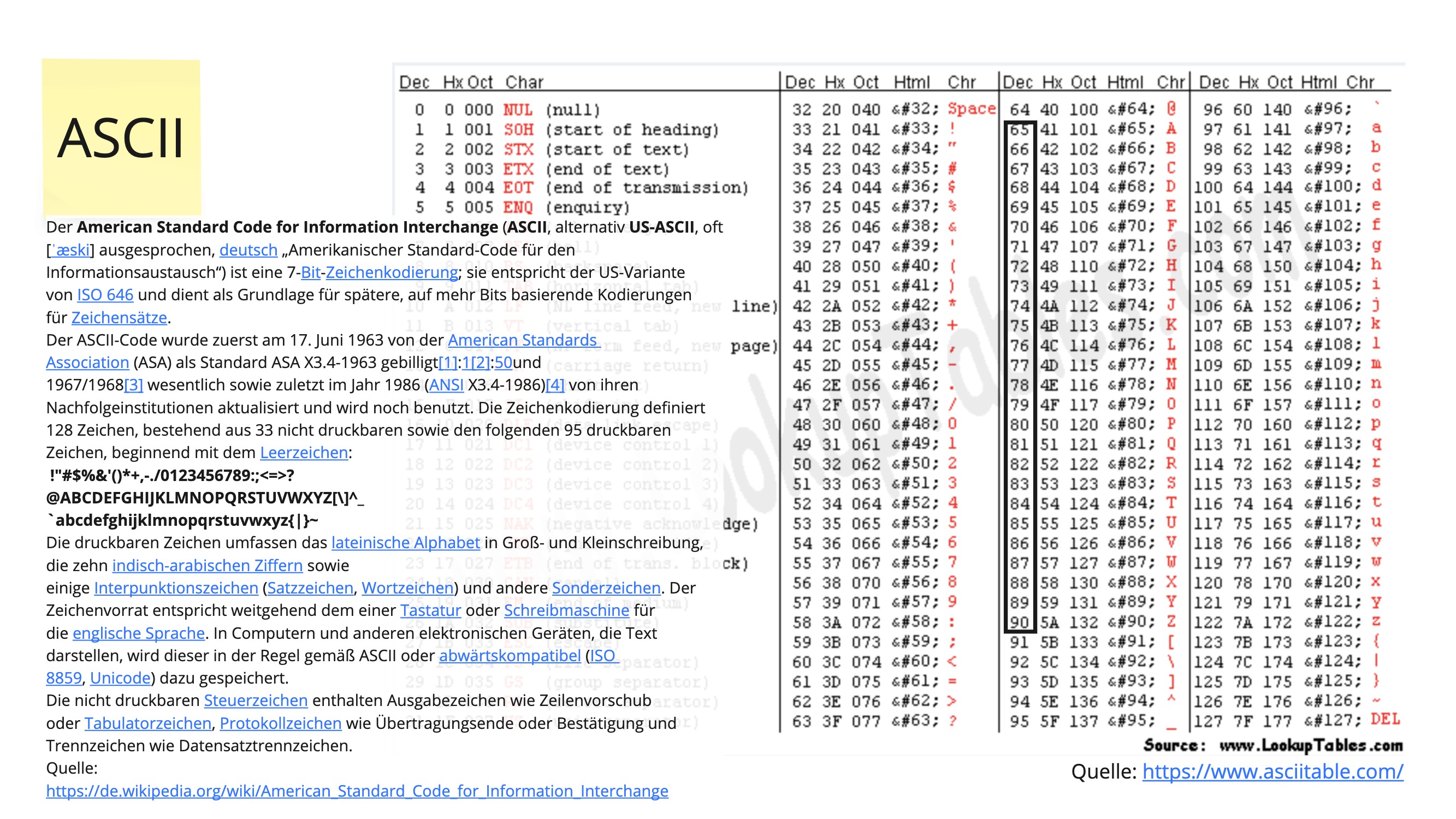
ASCII:

• Definition: American Standard Code for Information Interchange.
• Zeichensatz: 128 Zeichen (Ziffern, Buchstaben, Steuerzeichen).
• Größe: 7-Bit, häufig als 8-Bit gespeichert.
• Anwendung: Grundlegende Zeichenkodierung für englische Texte.

UTF-8:

• Definition: Unicode Transformation Format, 8-Bit.
• Zeichensatz: Kodiert alle Unicode-Zeichen.
• Größe: Variable Länge (1 bis 4 Byte pro Zeichen).
• Vorteil: Rückwärtskompatibel mit ASCII, speichereffizient bei ASCII-Zeichen.

UTF-16:

• Definition: Unicode Transformation Format, 16-Bit.
• Zeichensatz: Kodiert alle Unicode-Zeichen.
• Größe: Variable Länge (2 oder 4 Byte pro Zeichen).
• Anwendung: Häufig in Programmiersprachen und Betriebssystemen.

UTF-32:

• Definition: Unicode Transformation Format, 32-Bit.
• Zeichensatz: Kodiert alle Unicode-Zeichen.
• Größe: Feste Länge (4 Byte pro Zeichen).
• Vorteil: Direkter Zugriff auf Zeichen, aber speicherintensiv.

Nochmal zum Nachlesen...

Ein Byte besteht aus 8 Bits und kann 256 verschiedene Werte darstellen (von 0 bis 255). Bytes werden verwendet, um Daten, einschließlich Text, in Computern zu speichern.

ASCII

• ASCII (American Standard Code for Information Interchange) ist ein älterer Standard, der jedem Buchstaben, Zahl und Symbol eine Zahl im Bereich von 0 bis 127 zuordnet (also 7 Bits).
  • Beispiel: Der Buchstabe „A“ hat den ASCII-Wert 65.
• ASCII kann nur englische Zeichen und einige Steuerzeichen darstellen, was für viele Sprachen und Symbole nicht ausreicht.

UTF-8

• UTF-8 ist eine variable Länge Codierung für Unicode, die 1 bis 4 Bytes pro Zeichen verwendet.
  • Zeichen, die in ASCII enthalten sind, werden mit einem Byte kodiert (die Werte 0 bis 127).
  • Komplexere Zeichen (z.B. viele nicht-lateinische Zeichen oder Emojis) benötigen mehr Bytes.
• UTF-8 ist rückwärtskompatibel mit ASCII und sehr speichereffizient für Texte, die hauptsächlich aus ASCII-Zeichen bestehen.

UTF-16

• UTF-16 verwendet 2 oder 4 Bytes pro Zeichen.
  • Die meisten häufig verwendeten Zeichen (z.B. lateinische Buchstaben) werden mit 2 Bytes kodiert.
  • Seltenere Zeichen, wie bestimmte asiatische Schriftzeichen oder Emojis, benötigen 4 Bytes.
• UTF-16 wird oft in internen Systemen von Betriebssystemen verwendet, z.B. Windows.

UTF-32

• UTF-32 verwendet immer 4 Bytes pro Zeichen.
  • Dies macht die Verarbeitung einfacher, da jedes Zeichen die gleiche Größe hat, ist aber weniger speichereffizient, da auch einfache Zeichen, die nur ein Byte benötigen würden, 4 Bytes belegen.
• UTF-32 wird selten verwendet, außer in speziellen Fällen, in denen konstante Speicherplatzanforderungen für jedes Zeichen benötigt werden.

Tabellarische Darstellung von Zeichen in ASCII, UTF-8, UTF-16 und UTF-32

Die folgende Tabelle zeigt, wie verschiedene Zeichen in den Codierungen ASCII, UTF-8, UTF-16, und UTF-32 dargestellt werden.

Zeichen	ASCII	UTF-8 (Hex)	UTF-16 (Hex)	UTF-32 (Hex)
A	65	41	0041	00000041
B	66	42	0042	00000042
Z	90	5A	005A	0000005A
a	97	61	0061	00000061
0	48	30	0030	00000030
#	35	23	0023	00000023
©	Nicht verfügbar	C2 A9	00A9	000000A9
€	Nicht verfügbar	E2 82 AC	20AC	000020AC
你 (chinesisches Zeichen)	Nicht verfügbar	E4 BD A0	4F60	00004F60
😊 (Smiley Emoji)	Nicht verfügbar	F0 9F 98 8A	D83D DE0A	0001F60A

Nochmal zum Nachlesen...

Erklärung der Tabelle:

1. ASCII: Zeichen von 0 bis 127 sind verfügbar. Zeichen wie ©, €, chinesische Schriftzeichen oder Emojis sind nicht im ASCII-Standard enthalten.
2. UTF-8: UTF-8 verwendet eine variable Anzahl von Bytes. ASCII-Zeichen (wie A) werden mit einem Byte dargestellt, während komplexere Zeichen wie © und € mehr Bytes benötigen.
3. UTF-16: UTF-16 verwendet 2 Bytes (z.B. A) oder 4 Bytes für komplexere Zeichen (z.B. das Emoji 😊).
4. UTF-32: UTF-32 verwendet immer 4 Bytes pro Zeichen, unabhängig von der Komplexität des Zeichens.

Beispiele für Textdarstellungen:

• ASCII Beispiel:

  • Der Text "Hello" würde in ASCII folgendermaßen dargestellt:
    • H = 72, e = 101, l = 108, l = 108, o = 111.
    • Als Byte-Sequenz: 72 101 108 108 111 (dezimal).

• UTF-8 Beispiel:

  • Der Text "Hello" bleibt im UTF-8 identisch, da UTF-8 rückwärtskompatibel mit ASCII ist:
    • H = 48 65 6C 6C 6F (hexadezimal).
  • Für den Text „© 2024“ würde die UTF-8-Darstellung folgendermaßen aussehen:
    • C2 A9 32 30 32 34 (hexadezimal).

• UTF-16 Beispiel:

  • Der Text „Hello“ in UTF-16:
    • 0048 0065 006C 006C 006F (hexadezimal).
  • Für den Text „你好“ (chinesisch für „Hallo“) würde die UTF-16-Darstellung folgendermaßen aussehen:
    • 4F60 597D (hexadezimal).

• UTF-32 Beispiel:

  • Der Text „Hello“ in UTF-32:
    • 00000048 00000065 0000006C 0000006C 0000006F (hexadezimal).
  • Für den Text „😊“ (Smiley Emoji) würde die UTF-32-Darstellung folgendermaßen aussehen:
    • 0001F60A (hexadezimal).

Fazit:

• ASCII eignet sich gut für einfache englische Texte, ist aber begrenzt in der Zeichenvielfalt.
• UTF-8 ist eine flexible Codierung und der Standard im Web, da es effizient für ASCII-Texte ist und gleichzeitig internationale Zeichen unterstützt.
• UTF-16 ist in vielen Betriebssystemen und Programmiersprachen verbreitet, insbesondere in Windows.
• UTF-32 wird seltener verwendet, bietet jedoch eine konstante Größe für jedes Zeichen, was in bestimmten technischen Anwendungsfällen nützlich sein kann.

ASCII Tabelle